Significado de Intervalo de Confiança

O que significa Intervalo de Confiança

É uma estimativa de um intervalo utilizado na estatística, que contém um parâmetro populacional. Esse parâmetro de população desconhecido é encontrado através de um modelo de amostra calculado a partir dos dados recolhidos.

Exemplo: a média de uma amostra recolhida x̅ pode ou não coincidir com a verdadeira média populacional μ. Para isso, é possível considerar um intervalo de médias amostrais onde esta média populacional possa estar contida. Quanto maior este intervalo, maior a probabilidade de isso ocorrer.

O intervalo de confiança é expresso em porcentagem, denominadas por nível de confiança, sendo 90%, 95% e 99% as mais indicadas. Na imagem abaixo, por exemplo, temos um intervalo de confiança de 90% entre seus limites superior e inferior (a e -a). 

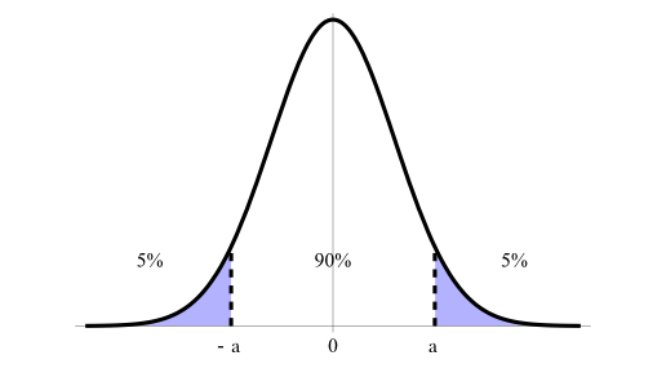Exemplo de Intervalo de Confiança de 90% entre seus limites superior (a) e inferior (-a). 

O Intervalo de Confiança é um dos conceitos mais importantes dentro dos testes de hipóteses na estatística, por ser utilizado como uma medida de incerteza. O termo foi introduzido pelo matemático e estatístico polonês Jerzy Neyman em 1937. 

Qual a relevância de um Intervalo de Confiança?

O intervalo de confiança é importante para indicar a margem de incerteza (ou imprecisão) frente a um cálculo efetuado. Esse cálculo usa a amostra do estudo para estimar o tamanho real do resultado na população de origem.

O cálculo de um intervalo de confiança é uma estratégia que considera a amostragem de erro. A dimensão do resultado do seu estudo e seu intervalo de confiança caracterizam os valores presumíveis para a população original. 

Quanto mais estreito for o intervalo de confiança, maior é a probabilidade da porcentagem da população de estudo representar o número real da população de origem dando maior certeza quanto ao resultado do objeto de estudo. 

Como interpretar um Intervalo de Confiança? 

A interpretação correta do intervalo de confiança é provavelmente o aspecto mais desafiador desse conceito estatístico. Um exemplo da interpretação mais comum do conceito é a seguinte:

Existe uma probabilidade de 95% de que, no futuro, o verdadeiro valor do parâmetro da população (por exemplo, média) caia no intervalo X (limite inferior) e Y (limite superior).  

Assim, interpreta-se o intervalo de confiança da seguinte maneira: é 95% confiante de que o intervalo entre X (limite inferior) e Y (limite superior) contém o verdadeiro valor do parâmetro populacional.  

Seria totalmente incorreto declarar que: há uma probabilidade de 95% de que o intervalo entre X (limite inferior) e Y (limite superior) contenha o valor real do parâmetro populacional.  

A afirmação acima é o equívoco mais comum sobre o intervalo de confiança. Depois que o intervalo estatístico é calculado, ele pode conter apenas o parâmetro da população ou não.

No entanto, os intervalos podem variar entre as amostras, enquanto o parâmetro da população verdadeira é o mesmo, independentemente da amostra.

Portanto, a declaração de probabilidade relativa ao intervalo de confiança pode ser feita somente no caso em que os intervalos de confiança são recalculados para o número de amostras.

As etapas do cálculo do Intervalo de Confiança 

O intervalo é calculado usando as seguintes etapas:

• Reúna os dados da amostra: n;
• Calcule a média da amostra x̅;
• Determine se um desvio padrão populacional (σ) é conhecido ou desconhecido;
• Se um desvio padrão populacional for conhecido, pode-se usar um ponto z para o nível de confiança correspondente;
• Se um desvio padrão populacional for desconhecido, podemos usar uma estatística t para o nível de confiança correspondente;
• Assim, encontram-se os limites inferior e superior do intervalo de confiança usando as seguintes fórmulas:

a) Desvio padrão de uma população conhecida: 

Fórmula para o cálculo de desvio padrão de uma população conhecida.

b) Desvio padrão de uma população desconhecida: 

Fórmula para o cálculo de desvio padrão de uma população desconhecida.

Exemplo prático de um intervalo de confiança 

Um estudo clínico avaliou a associação entre a presença de asma e o risco de desenvolvimento de Apneia Obstrutiva do Sono em adultos.

Alguns adultos foram recrutados aleatoriamente, dentro de uma lista de funcionários públicos do estado, para serem acompanhados ao longo de quatro anos.

Os participantes com asma, quando comparados com aqueles sem, tinham um risco maior de desenvolver a apneia em quatro anos.

Ao conduzir pesquisas clínicas como este exemplo, normalmente recruta-se um subgrupo da população de interesse para aumentar a eficiência do estudo (menos custos e menos tempo).

Este subgrupo de indivíduos, a população estudada, é constituído por aqueles que preenchem os critérios de inclusão e concordam em participar do estudo, como apresentado na imagem abaixo. 

Gráfico explicativo da população estudada no exemplo.

Em seguida, conclui-se o estudo e calcula-se um tamanho de efeito (por exemplo: uma diferença média ou um risco relativo) para responder à pergunta de pesquisa.

Este processo, denominado inferência, envolve o uso de dados coletados da população do estudo para estimar o tamanho do efeito real na população de interesse, ou seja, a população de origem.

No exemplo dado, os pesquisadores recrutaram uma amostra aleatória de funcionários do estado (população fonte) que foram elegíveis e concordaram em participar do estudo (população do estudo) e relataram que a asma aumenta o risco de desenvolver apneia na população estudada.

Para levar em conta um erro de amostragem devido ao recrutamento de apenas um subgrupo da população de interesse, eles também calcularam um intervalo de confiança de 95% (em torno da estimativa) de 1,06 - 1,82, indicando uma probabilidade de 95% de que o verdadeiro risco relativo na população de origem seria entre 1,06 e 1,82.

Intervalo de Confiança para média 

Quando se tem a informação do desvio padrão de uma população, pode-se calcular um intervalo de confiança para a média ou a média dessa população.

Quando uma característica estatística que está sendo medida (como renda, QI, preço, altura, quantidade ou peso) é numérica, na maioria dos casos estima-se encontrar o valor médio para a população.

Assim, procura-se encontrar a média populacional (μ) usando uma média de amostra (x̅), contando com uma margem de erro. O resultado desse cálculo é chamado de intervalo de confiança para a média da população.

Quando o desvio padrão da população é conhecido, a fórmula para um intervalo de confiança (IC) para uma média populacional é: 

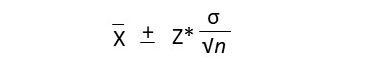
Onde: 

• x̅ é a média da amostra; 
• σ é o desvio padrão da população; 
• n é o tamanho da amostra; 
• Ζ* representa o valor apropriado da distribuição normal padrão para o seu nível de confiança desejado. 

Abaixo, seguem os valores para os vários níveis de confiança (Ζ*):

Nível de Confiança	Valor de Z*-
80%	1.28
90%	1.645 (convencional)
95%	1.96
98%	2.33
99%	2.58

A tabela acima mostra valores de z* para os níveis de confiança fornecidos. Observe que esses valores são obtidos da distribuição normal padrão (Z-).

A área entre cada valor z * e o negativo desse valor é a porcentagem de confiança (aproximada). Por exemplo, a área entre z * = 1,28 e z = -1,28 é aproximadamente 0,80. Portanto, essa tabela também pode ser expandida para outras porcentagens de confiança. A tabela mostra apenas as porcentagens de confiança mais usadas.

Veja também o significado de Hipótese. 

Fonte: Significados