Significado de Correlação

O que significa Correlação

Correlação significa uma semelhança ou relação entre duas coisas, pessoas ou ideias. É uma semelhança ou equivalência que existe entre duas hipóteses, situações ou objetos diferentes.

No campo da estatística e da matemática a correlação se refere a uma medida entre duas ou mais variáveis que se relacionam.

O termo correlação é um substantivo feminino que tem origem do latim correlatiōne. 

A palavra correlação pode ser substituída por sinônimos como: relação, equiparação, nexo, correspondência, analogia e conexão.

Coeficiente de Correlação

Na estatística o coeficiente de correlação de Pearson (r), que também é chamado de coeficiente de correlação produto-momento, mede a relação que existe entre duas variáveis dentro de uma mesma escala métrica.

A função do coeficiente de correlação é determinar qual é a intensidade da relação que existe entre conjuntos de dados ou informações conhecidas.

O valor do coeficiente de correlação pode variar entre -1 e 1 e o resultado obtido define se a correlação é negativa ou positiva.

Para interpretar o coeficiente é preciso saber que 1 significa que a correlação entre as variáveis é perfeita positiva e -1 significa que é perfeita negativa. Se o coeficiente for igual a 0 significa que as variáveis não dependem uma da outra.

Na estatística também existe o coeficiente de correlação Spearman, que tem esse nome em homenagem ao estatístico Charles Spearman. A função desse coeficiente é medir a intensidade da relação entre duas variáveis, sendo elas lineares ou não.

A correlação Spearman serve para avaliar se a intensidade da relação entre as duas variáveis analisadas pode ser medida por uma função monótona (função matemática que preserva ou inverte a relação de ordem inicial).

Cálculo do coeficiente de correlação de Pearson

Método 1) Cálculo do coeficiente de correlação de Pearson utilizando a covariância e o desvio padrão.

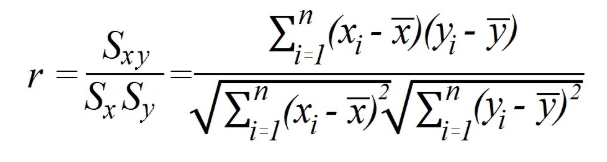
Onde

S_XY é a covariância;

S_x e S_y representam o desvio padrão, respectivamente, das variáveis x e y.

Neste caso, o cálculo passa por achar primeiro a covariância entre as variáveis, e o desvio padrão de cada uma delas. Depois, divide-se a covariância pela multiplicação dos desvios padrões.

Muitas vezes, o enunciado já fornece ou os desvios padrões das variáveis, ou a covariância entre elas, bastando só aplicar a fórmula.

Método 2) Cálculo do coeficiente de correlação de Pearson com dados em bruto (sem covariância ou desvio padrão).

Com este método, a fórmula mais direta é a seguinte:

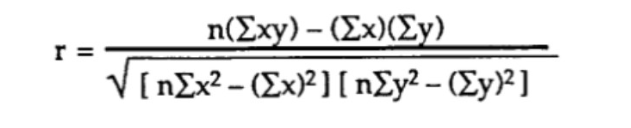
Por exemplo, assumindo que temos dados com n=6 observações de duas variáveis: nível de glicose(y) e idade (x), o cálculo segue as seguintes etapas:

Etapa 1) Construir a tabela com os dados existentes: i, x, y, e adicionar colunas em branco para xy, x² e y²:

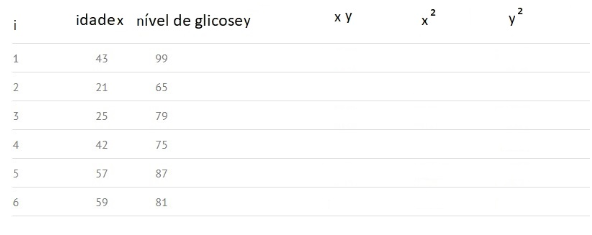
Etapa 2: Multiplicar x e y para preencher a coluna “xy”. Por exemplo, na linha 1 teremos: x1y1 = 43 × 99 = 4257.

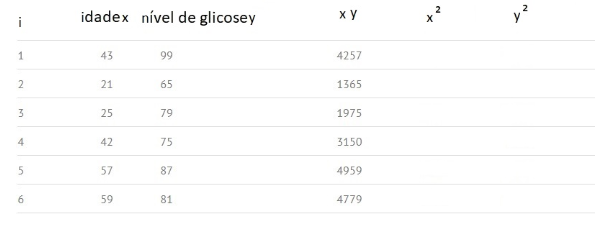
Etapa 3: Elevar ao quadrado os valores da coluna x, e registrar os resultados na coluna x². Por exemplo, na primeira linha teremos x₁² = 43 × 43 = 1849.

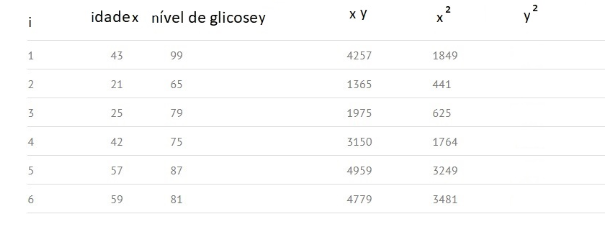
Etapa 4: Fazer o mesmo que na Etapa 3, utilizando agora a coluna y e registar o quadrado dos seus valores na coluna y². Por exemplo, na primeira linha teremos: y₁² = 99 × 99 = 9801.

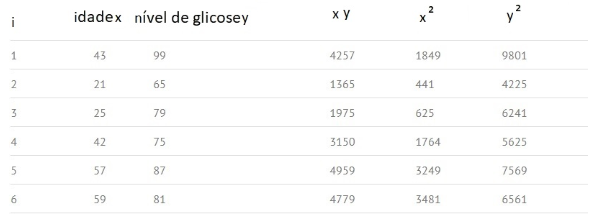
Etapa 5: Obter o somatório de todos os números das colunas e colocar o resultado no rodapé da coluna. Por exemplo, a soma da coluna Idade X é igual a 43+21+25+42+57+59 = 247.

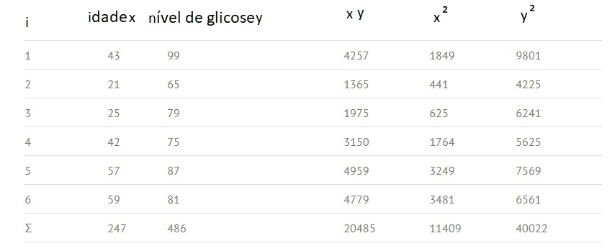
Etapa 6: Usar a fórmula referida para obter o coeficiente de correlação:

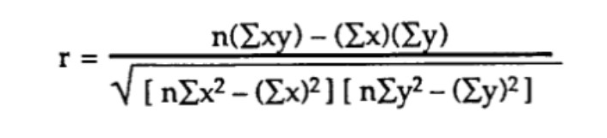
Assim, temos:

Cálculo do coeficiente de correlação de Spearman

O cálculo do coeficiente de correlação de Spearman é um pouco diferente. Para isso, precisamos de organizar os nossos dados na seguinte tabela:

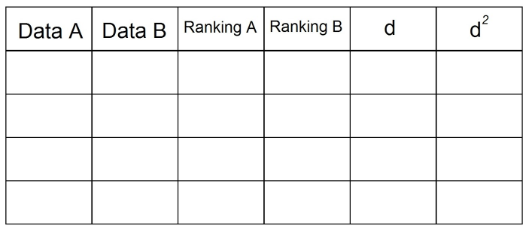
1. Tendo no enunciado 2 pares de dados, devemos introduzi-los na tabela. Por exemplo:

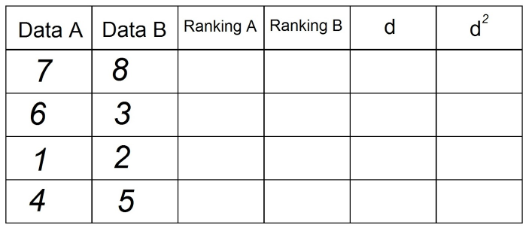
2. Na coluna “Ranking A” vamos classificar as observações que estão em “Data A” de forma crescente, sendo “1” o valor mais baixo da coluna, e n (número total de observações) o valor mais alto da coluna “Data A”. No nosso exemplo fica:

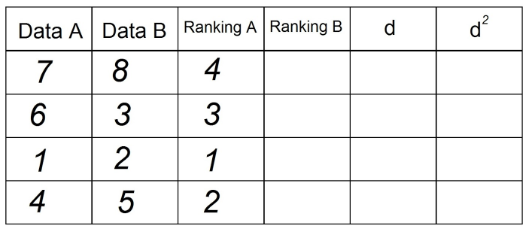
3. Fazemos o mesmo para obter a coluna “Ranking B”, utilizando agora as observações da coluna “Data B”:

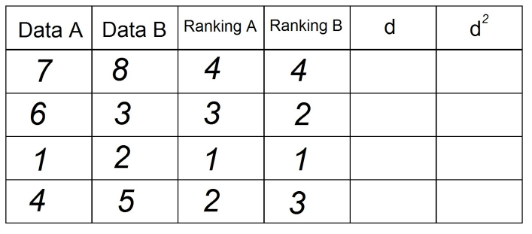
4. Na coluna “d” colocamos a diferença entre os dois Rankings (A - B). Aqui o sinal não importa.

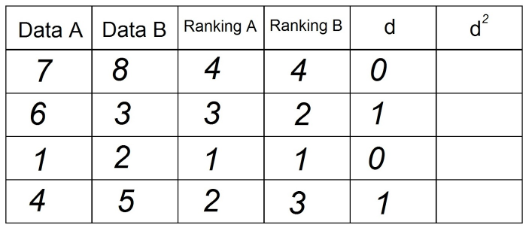
5. Elevar ao quadrado cada um dos valores da coluna “d” e registrar na coluna d²:

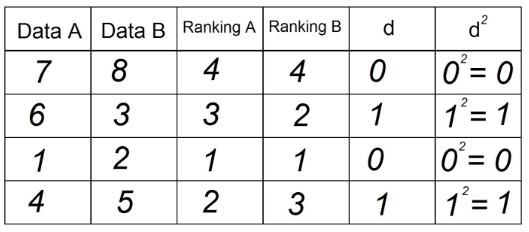
6. Somar todos os dados da coluna 'd²'. Esse valor é Σd². No nosso exemplo Σd² = 0+1+0+1 = 2

7. Agora utilizamos a fórmula de Spearman:

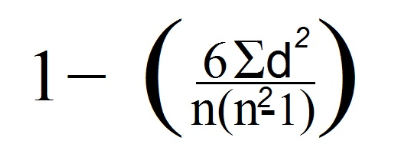
No nosso caso, n é igual a 4, pois olhamos para quantidade de linhas de dados (que corresponde ao número de observações).

8. Finalmente, substituímos os dados na fórmula anterior:

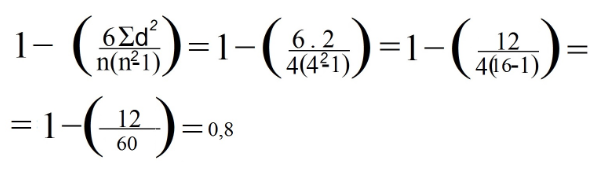
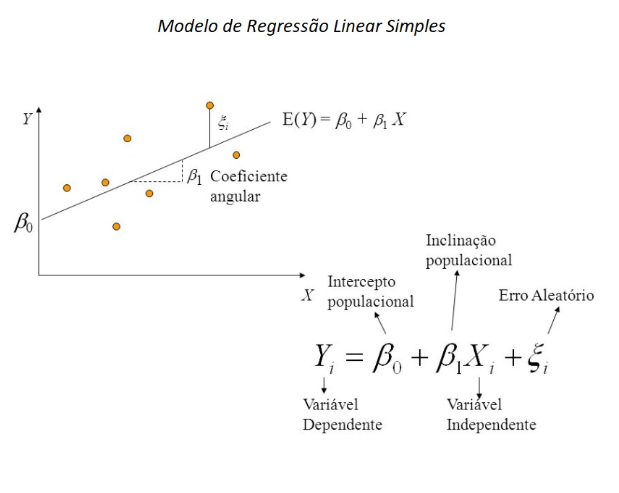
Regressão linear

A regressão linear é uma fórmula usada para fazer uma estimativa sobre o possível valor de uma variável (y) quando são conhecidos os valores de outras variáveis (x). O valor de 'x' é a variável independente ou explicativa e 'y' é a variável dependente ou resposta.

A regressão linear é usada para verificar como o valor de 'y' pode variar em função da variável 'x'. A reta que contém os valores da verificação da variação é chamada de reta de regressão linear.

Se a variável explicativa 'x' tiver um valor único, a regressão será chamada de regressão linear simples.

Fonte: Significados